Understanding Deterministic Finite Automata (DFA): Structure and Components

Introduction to Finite State Machines and Automata

Finite state machines, also known as finite automata, are fundamental concepts in the theory of computation. They serve as the simplest models of computation and are characterized by their limited memory capacity. Understanding these machines is crucial for anyone studying computer science or delving into the intricacies of computational theory.

Finite automata are broadly categorized into two main types:

1. Finite automata with output
   • Mealy machines
   • Moore machines
2. Finite automata without output
   • Deterministic Finite Automata (DFA)
   • Non-deterministic Finite Automata (NFA)
   • Epsilon Non-deterministic Finite Automata (ε-NFA)

In this article, we will focus primarily on Deterministic Finite Automata (DFA), exploring its structure, components, and formal definition.

Key Properties of Finite State Machines

Before diving into the specifics of DFAs, it's essential to remember two critical properties of finite state machines:

1. They represent the simplest model of computation.
2. They have very limited memory.

These properties make finite state machines ideal for certain types of computational tasks while limiting their applicability in more complex scenarios.

Deterministic Finite Automata (DFA): An Overview

Deterministic Finite Automata, or DFAs, are a specific type of finite state machine that plays a crucial role in computer science and formal language theory. To understand DFAs better, let's break down their structure and components.

Structure of a DFA

A DFA can be visualized as a directed graph with the following elements:

1. States: Represented by circles in the graph
2. Transitions: Represented by edges or arrows connecting the states
3. Inputs: Labels on the edges indicating the input that triggers a transition
4. Start State: Denoted by an arrow pointing to it from nowhere
5. Final State(s): Represented by double circles

Let's examine each of these components in detail.

Components of a DFA

States

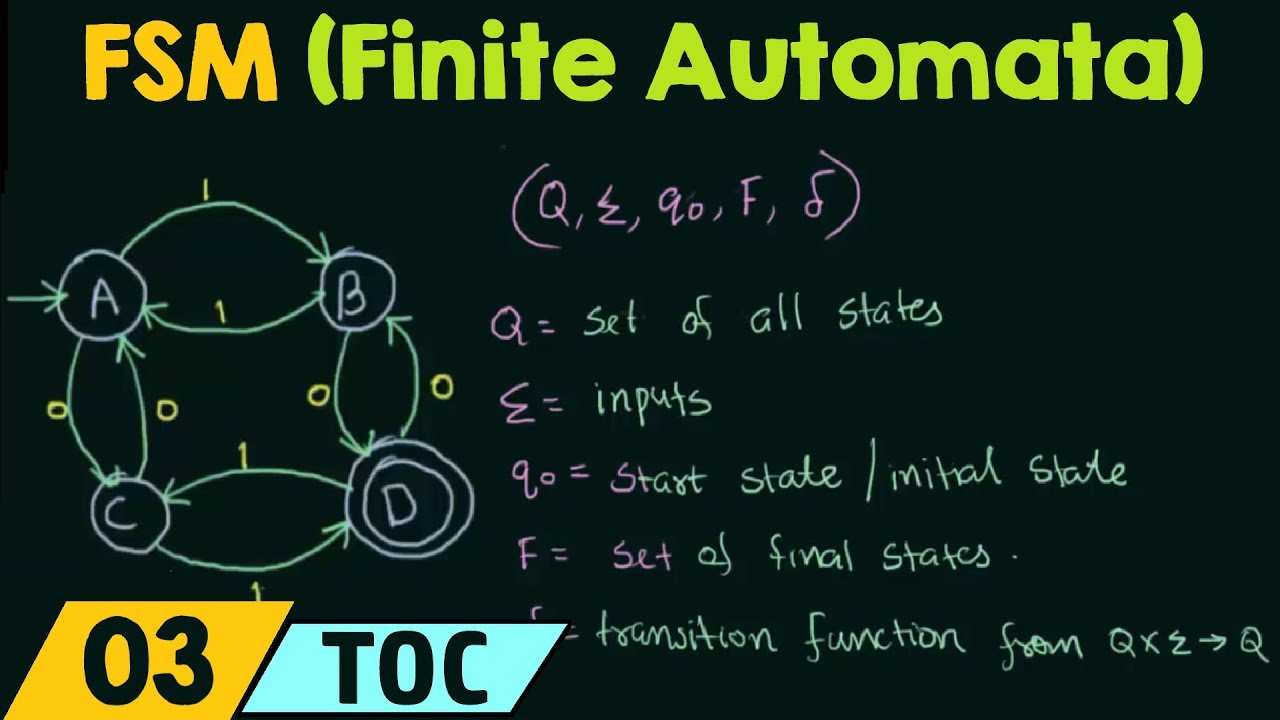
States are the fundamental building blocks of a DFA. They represent the different configurations or situations the machine can be in at any given time. In our example diagram, states are labeled as A, B, C, and D.

Transitions

Transitions show how the DFA moves from one state to another based on the input it receives. They are represented by arrows connecting different states.

Inputs

Inputs are the symbols or characters that the DFA processes. They are typically labeled on the transition arrows. In our example, the inputs are 0 and 1, representing a binary input alphabet.

Start State

The start state is where the DFA begins its operation. It is visually distinguished by an arrow pointing to it from nowhere. In our example diagram, state A is the start state.

Final State(s)

Final states, also known as accepting states, represent the successful completion of the DFA's task. They are depicted with double circles. In our example, state D is the final state.

Formal Definition of a DFA

A DFA is formally defined by a 5-tuple (Q, Σ, q0, F, δ), where:

• Q is the finite set of states
• Σ (Sigma) is the finite set of input symbols
• q0 is the initial state (q0 ∈ Q)
• F is the set of final states (F ⊆ Q)
• δ (delta) is the transition function that maps Q × Σ to Q

Let's apply this formal definition to our example DFA:

1. Q = {A, B, C, D}
2. Σ = {0, 1}
3. q0 = A
4. F = {D}
5. δ: The transition function

Transition Function (δ)

The transition function δ maps the current state and input symbol to the next state. It can be represented as a table:

State	Input 0	Input 1
A	C	B
B	D	A
C	A	D
D	B	C

This table shows all possible state transitions based on the current state and input symbol.

How a DFA Operates

To understand how a DFA operates, let's walk through an example:

1. The DFA starts in the initial state A.
2. It reads an input symbol (0 or 1).
3. Based on the current state and input symbol, it transitions to a new state according to the transition function.
4. This process continues until all input symbols are processed.
5. If the DFA ends in a final state after processing all inputs, the input string is accepted. Otherwise, it is rejected.

Importance and Applications of DFAs

DFAs have numerous applications in computer science and beyond:

1. Pattern Matching: DFAs are used in text editors and command-line interfaces for finding specific patterns or strings.

2. Lexical Analysis: Compilers use DFAs in the lexical analysis phase to recognize tokens in the source code.

3. Protocol Implementation: Network protocols often use DFAs to manage state transitions and ensure correct behavior.

4. Digital Circuit Design: DFAs help in designing sequential logic circuits and control systems.

5. Natural Language Processing: Some aspects of language processing, such as morphological analysis, can be modeled using DFAs.

6. Data Validation: DFAs can verify if input data conforms to specific patterns or formats.

7. Game Design: Simple game logic and character behavior can be modeled using DFAs.

Advantages and Limitations of DFAs

Advantages

1. Simplicity: DFAs are easy to understand and implement.
2. Efficiency: They process input in linear time, making them very fast.
3. Determinism: For any given input and current state, the next state is uniquely determined.
4. Equivalence to Regular Expressions: DFAs can represent any regular language, making them powerful tools in formal language theory.

Limitations

1. Limited Memory: DFAs cannot count or remember arbitrary amounts of information.
2. Finite States: They cannot handle languages that require an infinite number of states.
3. No Backtracking: Once a transition is made, a DFA cannot go back or reconsider its decision.

Comparison with Other Finite Automata

DFA vs. NFA

Non-deterministic Finite Automata (NFA) differ from DFAs in that they can have multiple possible next states for a given input and current state. While NFAs offer more flexibility in design, they are theoretically equivalent to DFAs in terms of the languages they can recognize.

DFA vs. ε-NFA

Epsilon Non-deterministic Finite Automata (ε-NFA) are similar to NFAs but also allow transitions without consuming an input symbol (ε-transitions). Like NFAs, ε-NFAs can be converted to equivalent DFAs, although the resulting DFA may have significantly more states.

Constructing DFAs

Constructing a DFA involves several steps:

1. Identify the alphabet: Determine the set of input symbols the DFA will process.
2. Define the states: Decide what states are necessary to represent the problem.
3. Determine the start state: Choose which state will be the initial state.
4. Identify the final states: Decide which states represent successful completion.
5. Create the transition function: Define how the DFA moves between states for each input.

Minimizing DFAs

DFA minimization is the process of reducing the number of states in a DFA while preserving its language recognition capabilities. This process is important for optimizing the efficiency of DFAs. Common minimization algorithms include:

1. Hopcroft's algorithm
2. Brzozowski's algorithm
3. Moore's algorithm

DFAs and Regular Languages

DFAs are closely related to regular languages. In fact, a language is regular if and only if it can be recognized by a DFA. This connection makes DFAs a powerful tool in formal language theory and compiler design.

Implementing DFAs in Programming

DFAs can be implemented in various programming languages. Here's a simple pseudocode representation of a DFA:

function runDFA(input_string):
    current_state = start_state
    for symbol in input_string:
        current_state = transition_function(current_state, symbol)
    return current_state in final_states

This basic structure can be adapted to implement specific DFAs for various applications.

Conclusion

Deterministic Finite Automata are fundamental structures in computer science and formal language theory. Their simplicity and efficiency make them valuable tools for a wide range of applications, from text processing to protocol design. By understanding the structure and components of DFAs, you gain insight into the foundations of computation and language recognition.

As you continue to explore the theory of computation, you'll encounter more complex automata and computational models. However, the principles you've learned about DFAs will serve as a solid foundation for understanding these advanced concepts. Whether you're a computer science student, a software engineer, or simply curious about the theoretical underpinnings of computation, mastering DFAs is an essential step in your journey through the fascinating world of computational theory.

Article created from: https://www.youtube.com/watch?v=Qa6csfkK7_I&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=3