Converting NFAs to DFAs: A Comprehensive Guide

Introduction to Finite Automata Conversion

In the world of theoretical computer science, finite automata play a crucial role in understanding and implementing various computational models. Two fundamental types of finite automata are Deterministic Finite Automata (DFA) and Non-deterministic Finite Automata (NFA). This article will delve into the process of converting NFAs to DFAs, providing a comprehensive understanding of the concept.

Understanding DFAs and NFAs

Before we dive into the conversion process, it's essential to grasp the key differences between DFAs and NFAs:

Deterministic Finite Automata (DFA)

A DFA is a finite state machine where:

• For each input symbol, there is exactly one transition from each state.
• The machine is always in a single, deterministic state.

Non-deterministic Finite Automata (NFA)

An NFA is a finite state machine where:

• For each input symbol, there can be zero, one, or multiple transitions from each state.
• The machine can be in multiple states simultaneously.

The Relationship Between DFAs and NFAs

It's important to note two key points about the relationship between DFAs and NFAs:

1. Every DFA is an NFA, but not every NFA is a DFA.
2. There exists an equivalent DFA for every NFA.

To justify these statements, let's examine the formal definitions of DFAs and NFAs:

DFA Definition

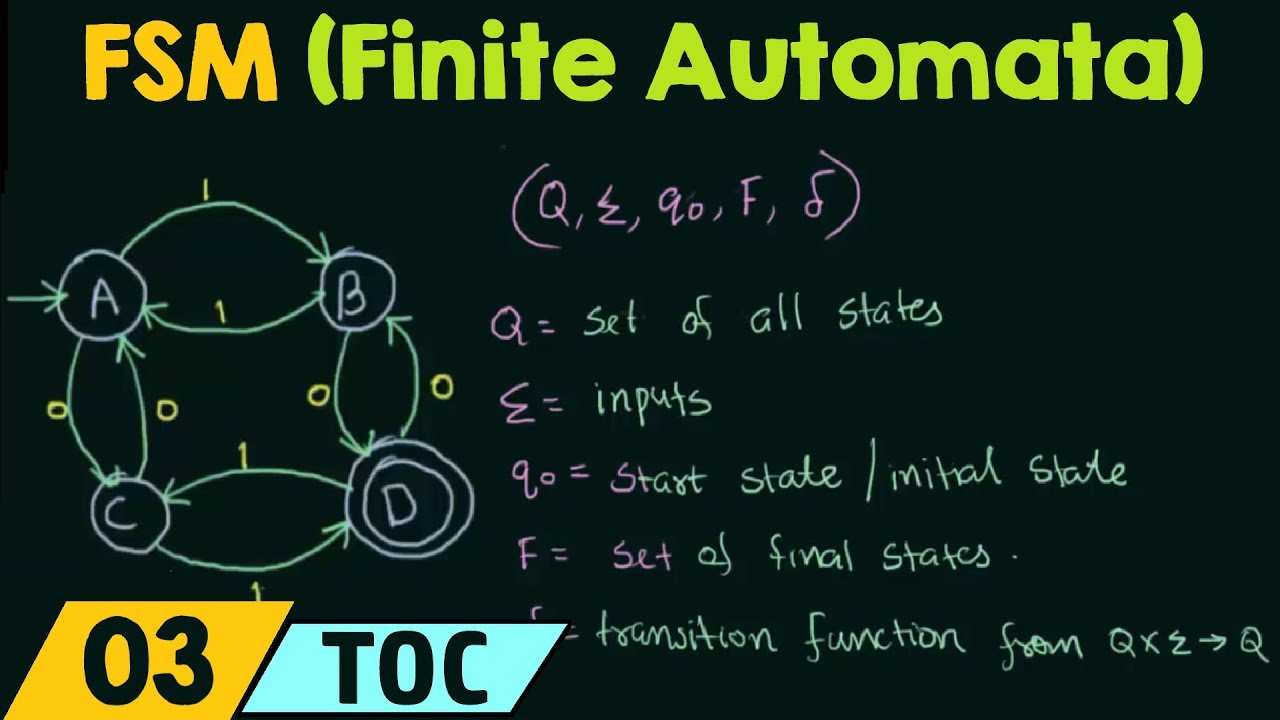
A DFA is defined using five tuples: (Q, Σ, δ, q0, F) Where:

• Q is a finite set of states
• Σ is a finite set of input symbols
• δ is the transition function that maps Q × Σ to Q
• q0 is the initial state
• F is the set of final states

NFA Definition

An NFA is also defined using five tuples: (Q, Σ, δ, q0, F) The key difference lies in the transition function:

• δ maps Q × Σ to 2^Q (the power set of Q)

Observing these definitions, we can see that the DFA's transition function (Q × Σ to Q) is a subset of the NFA's transition function (Q × Σ to 2^Q). This relationship explains why every DFA is an NFA, but not vice versa.

Converting NFA to DFA: A Step-by-Step Guide

Now that we understand the theoretical background, let's walk through the process of converting an NFA to its equivalent DFA using a practical example.

Example Language

Let's consider the following language: L = {set of all strings over {0,1} that start with 0}

Step 1: Design the NFA

First, we'll design an NFA for the given language:

1. Create a starting state A.
2. On input 0, transition from state A to state B.
3. Make state B the final (accepting) state.
4. In state B, on input 0 or 1, remain in state B.

Step 2: Create the NFA State Transition Diagram

Let's create a state transition diagram for our NFA:

State	Input 0	Input 1
A	B	ϕ
B	B	B

Note: ϕ represents the dead configuration in the NFA.

Step 3: Convert NFA to DFA

Now, we'll convert this NFA to its equivalent DFA:

1. Start with the initial state A.
2. For each state and input combination, determine the set of possible next states.
3. Create new states in the DFA for each unique set of NFA states.
4. Continue this process until no new states are created.

Let's create the DFA state transition diagram:

State	Input 0	Input 1
A	B	C
B	B	B
C	C	C

Note: State C is the dead state (trap state) in the DFA, equivalent to the ϕ configuration in the NFA.

Step 4: Draw the DFA Diagram

Based on the state transition diagram, we can now draw the complete DFA:

• State A is the starting state.
• State B is the final (accepting) state.
• State C is the dead state.
• Transitions:
  • A to B on input 0
  • A to C on input 1
  • B to B on inputs 0 and 1
  • C to C on inputs 0 and 1

Key Differences Between NFA and DFA

Let's highlight some key differences between the NFA and its equivalent DFA:

1. Number of states: The DFA may have more states than the original NFA. In our example, we added a new state C.

2. Determinism: In the DFA, each state has exactly one transition for each input symbol, making it deterministic.

3. Dead state: The DFA explicitly includes a dead state (C), which replaces the ϕ configuration in the NFA.

4. Completeness: The DFA is complete, meaning it defines transitions for all possible input symbols from every state.

Advantages of Converting NFA to DFA

Converting an NFA to a DFA offers several advantages:

1. Simplicity: DFAs are easier to implement and simulate in computer programs.

2. Efficiency: DFAs generally provide faster string recognition compared to NFAs.

3. Determinism: The deterministic nature of DFAs makes them more predictable and easier to analyze.

4. Minimization: DFAs can be further optimized through minimization techniques, potentially reducing the number of states.

Applications of NFA to DFA Conversion

The process of converting NFAs to DFAs has numerous practical applications in computer science and software engineering:

1. Regular Expression Processing: Many text editors and search tools use finite automata to implement regular expression matching. Converting NFAs to DFAs can optimize these processes.

2. Lexical Analysis: Compilers and interpreters often use DFAs in their lexical analysis phase to tokenize input source code efficiently.

3. Network Protocol Validation: Finite automata are used to model and validate network protocols. Converting NFAs to DFAs can help in creating more efficient validation systems.

4. Pattern Matching: Many string matching algorithms utilize finite automata. DFAs derived from NFAs can improve the performance of these algorithms.

5. Natural Language Processing: Some NLP tasks, such as tokenization and simple parsing, can benefit from the use of DFAs converted from NFAs.

Advanced Concepts in NFA to DFA Conversion

While we've covered the basic process of converting NFAs to DFAs, there are several advanced concepts and techniques worth exploring:

Subset Construction Algorithm

The subset construction algorithm, also known as the powerset construction, is a formal method for converting an NFA to a DFA. This algorithm systematically creates DFA states that correspond to sets of NFA states.

Steps of the subset construction algorithm:

1. Start with the initial state of the NFA.
2. For each set of NFA states, compute the ε-closure (if ε-transitions are present).
3. For each input symbol, compute the set of possible next states.
4. Create a new DFA state for each unique set of NFA states encountered.
5. Continue this process until no new sets of NFA states are generated.

ε-NFA to DFA Conversion

Some NFAs include ε-transitions, which allow state changes without consuming an input symbol. Converting an ε-NFA to a DFA involves an additional step of computing ε-closures for each state before applying the subset construction algorithm.

State Explosion

One potential drawback of NFA to DFA conversion is the state explosion problem. In the worst case, if an NFA has n states, the equivalent DFA may have up to 2^n states. This exponential growth can lead to practical limitations for very large NFAs.

Lazy Construction

To mitigate the state explosion problem, lazy construction techniques can be employed. Instead of generating all possible DFA states upfront, states are created on-demand as needed during the automaton's operation.

Best Practices for NFA to DFA Conversion

When working with NFA to DFA conversion in practice, consider the following best practices:

1. Optimize the NFA first: Before conversion, try to simplify and optimize the NFA by removing unnecessary states and transitions.

2. Use efficient data structures: Implement the conversion algorithm using appropriate data structures (e.g., hash tables) to improve performance.

3. Consider lazy construction: For large NFAs, implement lazy construction to avoid generating unnecessary states.

4. Minimize the resulting DFA: After conversion, apply DFA minimization algorithms to reduce the number of states in the final automaton.

5. Test thoroughly: Verify the correctness of the converted DFA by testing it with various input strings, including edge cases.

Conclusion

Converting NFAs to DFAs is a fundamental concept in the theory of computation with significant practical implications. By understanding this process, computer scientists and software engineers can design more efficient algorithms and systems for tasks involving regular languages and pattern matching.

The conversion process, while sometimes resulting in an increase in the number of states, provides a deterministic and often more efficient automaton for string recognition tasks. As we've seen, the process involves carefully mapping out state transitions and creating new states to handle the non-deterministic aspects of the original NFA.

Mastering NFA to DFA conversion opens up a world of possibilities in various domains, from compiler design to text processing and beyond. By applying the principles and techniques discussed in this article, you'll be well-equipped to tackle complex automata-related problems and optimize your solutions for real-world applications.

Remember that while the basic conversion process is straightforward, there are always opportunities for optimization and refinement. As you work with more complex automata, consider exploring advanced techniques like lazy construction and efficient minimization algorithms to further improve your implementations.

With a solid understanding of NFA to DFA conversion, you're now ready to apply this knowledge to solve practical problems and delve deeper into the fascinating world of formal languages and automata theory.

Article created from: https://www.youtube.com/watch?v=--CSVsFIDng&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=15