Understanding Theory of Computation: From Finite State Machines to Undecidable Problems

Introduction to Theory of Computation

Theory of Computation is a cornerstone course in computer science, offering profound insights into the capabilities and limitations of computational systems. While it may not directly teach programming or hardware design, it provides a crucial understanding of how computer scientists have approached the field as a science over the past five decades.

What is Theory of Computation?

At its core, Theory of Computation addresses three fundamental questions:

1. What can be computed mechanically?
2. How fast can computations be performed?
3. How much space is required for these computations?

This course delves into the types of problems that machines can solve, as well as those that remain beyond the reach of computational systems. By exploring these concepts, students gain a deeper appreciation for the power and limitations of computers.

Key Concepts in Computational Theory

Mechanical Computation: A Simple Example

To illustrate the concept of mechanical computation, let's consider a basic example:

Imagine designing a machine that accepts all binary strings ending in zero. For instance, given the string "11101011", the machine would scan the last digit. If it's zero, the string is accepted; if it's one, the string is rejected.

This simple example demonstrates how a machine can be programmed to make decisions based on specific criteria.

More Complex Computations

Moving beyond basic string recognition, let's consider a more sophisticated example: designing a machine that accepts all valid Java code.

In this case, the machine would need to check the binary equivalent of the code and determine whether it represents valid Java syntax. This is precisely what compilers do - they analyze code, flag errors, and only execute valid programs.

This example highlights how Theory of Computation principles underpin essential tools in software development, such as compiler design.

Limitations of Computation

While many computational tasks are achievable, some problems remain beyond the reach of mechanical computation. Consider a hypothetical system designed to accept all valid Java code that never enters an infinite loop.

Creating such a system is impossible. This example introduces the concept of undecidable problems - computational tasks that no algorithm can solve with certainty.

The Essence of Computational Theory

At its heart, Theory of Computation involves designing systems or machines that:

1. Receive input
2. Process that input based on predefined rules
3. Produce a binary output (accept or reject)

This framework forms the basis for studying various computational models and their capabilities.

Layers of Computational Theory

Theory of Computation is structured into several layers, each representing a different level of computational power and complexity:

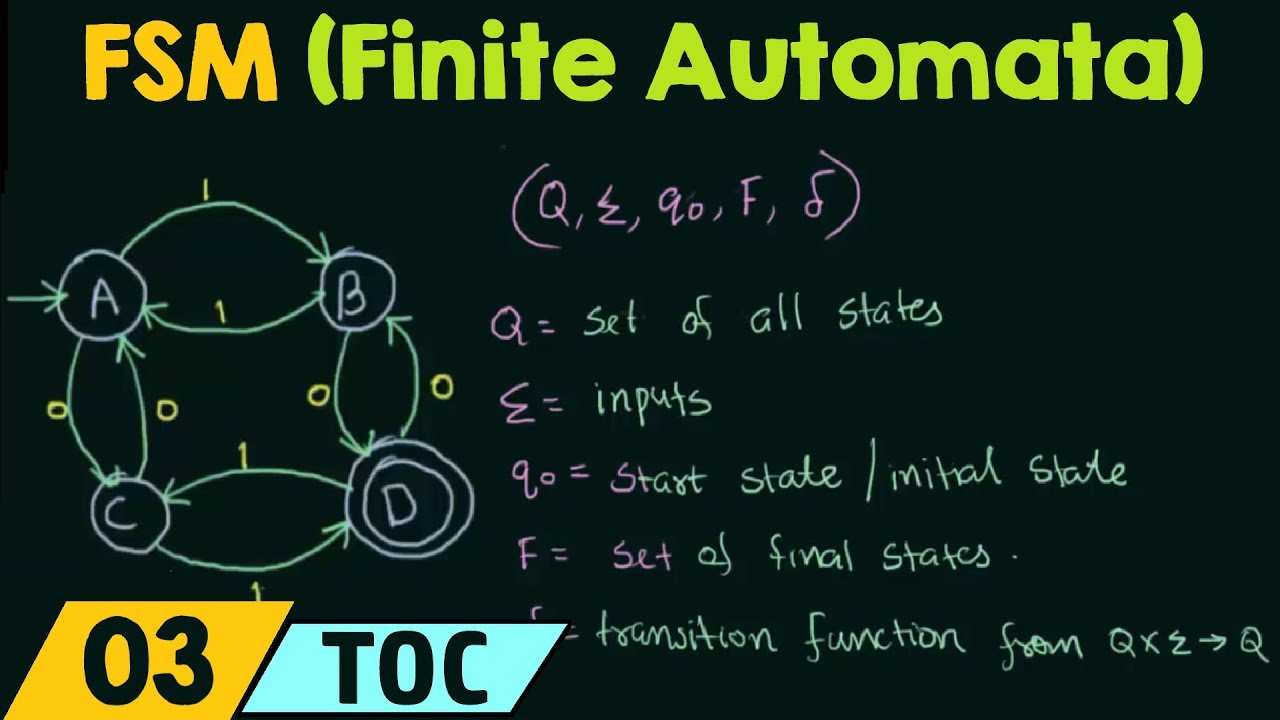
1. Finite State Machines (FSM)

Finite State Machines represent the simplest model of computation. They have extremely limited memory and can only perform basic, low-level computations. Despite their simplicity, FSMs serve as the foundational building block for more complex computational models.

Key characteristics of FSMs include:

• Limited number of states
• Transitions between states based on input
• No memory beyond the current state

FSMs find applications in various fields, including:

• Digital circuit design
• Pattern matching in text processing
• Simple game AI
• Protocol implementation in networking

2. Context-Free Languages (CFL)

Context-Free Languages represent a step up in computational power from FSMs. They can handle more complex patterns and structures in data.

Important points about CFLs:

• More expressive than regular languages (which FSMs can process)
• Can handle nested structures
• Widely used in parsing and compiler design

Applications of CFLs include:

• Parsing programming languages
• Natural language processing
• XML and HTML parsing
• Mathematical expression evaluation

3. Turing Machines

Named after Alan Turing, who conceptualized them in 1936, Turing Machines represent a significant leap in computational power. They can perform high-level computations and are considered the theoretical basis for modern computers.

Key features of Turing Machines:

• Unlimited memory (in theory)
• Can simulate any computer algorithm
• Used to define computational complexity classes

Implications of Turing Machines:

• Basis for understanding algorithm complexity
• Foundational in proving limits of computation
• Instrumental in defining the Church-Turing thesis

4. Undecidable Problems

The final layer deals with problems that cannot be solved algorithmically. These are known as undecidable problems.

Characteristics of undecidable problems:

• No algorithm can solve them for all possible inputs
• Often involve self-referential or infinitely recursive scenarios
• Help define the boundaries of what is computationally possible

Examples of undecidable problems:

• The Halting Problem (determining if a program will finish running or continue indefinitely)
• Rice's Theorem (making non-trivial decisions about program behavior)
• Post's Correspondence Problem

Practical Applications of Computational Theory

While Theory of Computation may seem abstract, its principles have wide-ranging applications in computer science and software engineering:

1. Compiler Design

Theory of Computation forms the backbone of compiler design. Concepts like finite state machines and context-free grammars are essential in lexical analysis and parsing phases of compilation.

2. Regular Expressions

Regular expressions, widely used in text processing and pattern matching, are based on the theory of regular languages and finite automata.

3. Formal Verification

Formal methods for verifying software and hardware correctness rely heavily on concepts from Theory of Computation.

4. Cryptography

Many cryptographic protocols and algorithms are based on computational complexity theory, a branch of Theory of Computation.

5. Artificial Intelligence

Certain AI techniques, particularly in natural language processing and machine learning, utilize concepts from formal language theory.

The Importance of Theory of Computation in Computer Science Education

Understanding Theory of Computation is crucial for several reasons:

1. Foundational Knowledge: It provides a theoretical foundation for understanding the capabilities and limitations of computers.

2. Problem-Solving Skills: Studying computational theory enhances logical thinking and problem-solving abilities.

3. Algorithm Analysis: It offers tools for analyzing algorithm efficiency and complexity.

4. Innovation: Knowledge of computational limits can inspire creative solutions to complex problems.

5. Interdisciplinary Applications: Concepts from Theory of Computation find applications in fields like linguistics, biology, and physics.

Challenges in Learning Theory of Computation

Despite its importance, many students find Theory of Computation challenging:

1. Abstraction: The course deals with abstract concepts that may seem disconnected from practical programming.

2. Mathematical Nature: It involves formal proofs and mathematical reasoning, which can be daunting for some students.

3. Conceptual Leaps: Moving between different models of computation requires significant conceptual understanding.

4. Limited Immediate Application: Unlike programming courses, the practical applications may not be immediately obvious.

Strategies for Mastering Theory of Computation

To succeed in studying Theory of Computation:

1. Build Strong Foundations: Ensure a solid understanding of basic discrete mathematics and logic.

2. Visualize Concepts: Use diagrams and simulations to visualize abstract concepts like state machines.

3. Practice Problems: Regularly solve problems to reinforce theoretical concepts.

4. Seek Real-World Connections: Try to relate theoretical concepts to practical applications in computer science.

5. Collaborative Learning: Discuss concepts with peers to gain different perspectives and deepen understanding.

6. Incremental Learning: Start with simpler models like FSMs before moving to more complex concepts.

Future Directions in Computational Theory

As technology evolves, new areas of research in Theory of Computation are emerging:

1. Quantum Computation: Exploring the theoretical foundations of quantum computers and their capabilities.

2. Bio-inspired Computation: Investigating computational models inspired by biological systems.

3. Machine Learning Theory: Developing theoretical frameworks for understanding and improving machine learning algorithms.

4. Complexity Theory: Ongoing research into P vs NP problem and other fundamental questions in computational complexity.

5. Algorithmic Game Theory: Studying the intersection of game theory and algorithm design.

Conclusion

Theory of Computation, while challenging, offers invaluable insights into the fundamental nature of computation. From the basic building blocks of finite state machines to the mind-bending concepts of undecidable problems, this field provides a comprehensive framework for understanding what computers can and cannot do.

As we progress through the layers of computational theory - from FSMs to CFLs, Turing Machines, and beyond - we gain a deeper appreciation for the power and limitations of computational systems. This knowledge not only enhances our understanding of computer science but also equips us with powerful tools for problem-solving and innovation in the digital age.

Whether you're a computer science student, a software engineer, or simply curious about the theoretical underpinnings of modern technology, exploring Theory of Computation offers a fascinating journey into the heart of computational thinking. It challenges us to think beyond the practical aspects of programming and consider the fundamental nature of computation itself, paving the way for future innovations and discoveries in the ever-evolving world of computer science.

Article created from: https://www.youtube.com/watch?v=58N2N7zJGrQ&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=1