Understanding Nondeterministic Finite Automata (NFA): A Comprehensive Guide

Introduction to Finite Automata

In the realm of computer science and computational theory, finite automata play a crucial role in understanding language recognition and processing. These abstract machines serve as fundamental models for studying the behavior of systems with a finite number of states. Among the various types of finite automata, two prominent categories stand out: Deterministic Finite Automata (DFA) and Nondeterministic Finite Automata (NFA).

Deterministic Finite Automata (DFA): A Brief Overview

Before delving into the intricacies of Nondeterministic Finite Automata, it's essential to understand the basics of Deterministic Finite Automata. A DFA is a mathematical model of computation that processes input strings and makes state transitions based on the current state and the input symbol.

Key characteristics of a DFA include:

1. Deterministic nature: For each input symbol and current state, there is exactly one next state.
2. Finite set of states: The automaton has a limited number of internal states.
3. Input-driven transitions: State changes occur based on the input symbols.
4. Acceptance criteria: The automaton accepts or rejects input strings based on whether the final state is an accepting state.

DFAs are widely used in various applications, including lexical analysis in compilers, pattern matching, and protocol verification.

Introducing Nondeterministic Finite Automata (NFA)

Nondeterministic Finite Automata (NFA) represent an extension of the DFA concept, introducing a level of unpredictability in state transitions. Unlike DFAs, where the next state is always determined, NFAs allow for multiple possible next states or even no next state for a given input symbol and current state.

Key Features of NFAs

1. Multiple transition options: For a given input symbol and current state, an NFA can have zero, one, or multiple possible next states.
2. Epsilon transitions: NFAs can make transitions without consuming an input symbol, known as epsilon (ε) transitions.
3. Acceptance criteria: An NFA accepts a string if there exists at least one path from the start state to an accepting state that consumes the entire input.

Formal Definition of an NFA

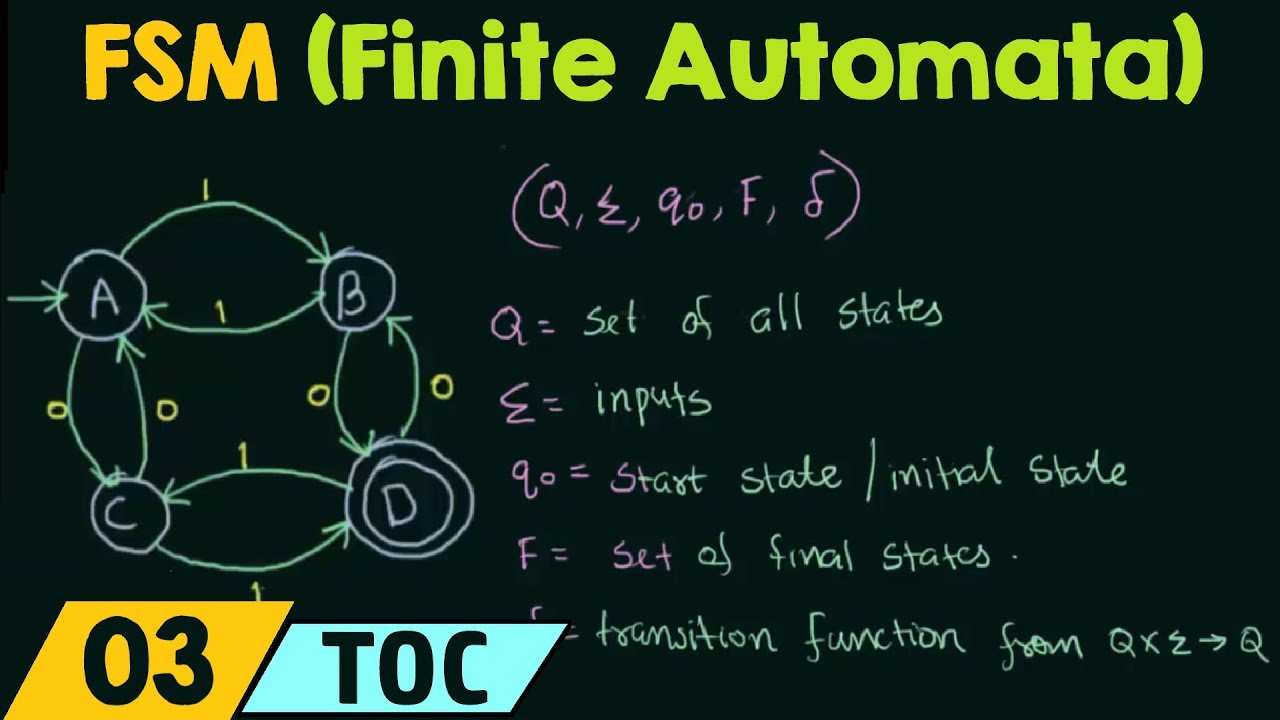
An NFA is formally defined as a 5-tuple (Q, Σ, δ, q0, F), where:

• Q is a finite set of states
• Σ is a finite set of input symbols (alphabet)
• δ is the transition function: Q × (Σ ∪ {ε}) → P(Q), where P(Q) is the power set of Q
• q0 ∈ Q is the start state
• F ⊆ Q is the set of accept (final) states

This formal definition highlights the key differences between NFAs and DFAs, particularly in the transition function and the inclusion of epsilon transitions.

Understanding NFA State Diagrams

State diagrams provide a visual representation of NFAs, making it easier to understand their behavior. Let's examine some examples to illustrate the unique properties of NFAs.

Example 1: NFA Accepting Strings with '1' in the Third-to-Last Position

Consider an NFA that accepts any string containing a '1' in the third position from the end. The state diagram for this NFA might look like this:

   ┌─────┐    1     ┌─────┐    0,1   ┌─────┐    0,1   ┌─────┐
-->│ q0  │───────-->│ q1  │───────-->│ q2  │───────-->│ q3  │
   └─────┘    ↺     └─────┘          └─────┘          └─────┘
     │ 0,1                                              (accept)
     │
     ▼

In this diagram:

• State q0 can transition to itself on 0 or 1, or move to q1 on reading a 1.
• Once in q1, the NFA must read two more symbols to reach the accepting state q3.
• The NFA accepts strings like "111" and "1100", but rejects "1000" and "1011".

Example 2: NFA Accepting Strings Ending with '0'

Let's consider another NFA that accepts any string ending with '0':

   ┌─────┐    0,1   ┌─────┐    0    ┌─────┐
-->│ q0  │───────-->│ q1  │───────>│ q2  │
   └─────┘    ↺     └─────┘         └─────┘
                                    (accept)

In this NFA:

• State q0 can transition to itself on any input (0 or 1).
• From q0 or q1, the NFA can move to q1 on any input.
• The transition from q1 to q2 (accept state) occurs only on reading a '0'.

This NFA demonstrates how nondeterminism allows for simpler state diagrams compared to equivalent DFAs.

The Power of Epsilon Transitions

One of the unique features of NFAs is their ability to make epsilon (ε) transitions. These are transitions that don't consume any input symbol, allowing the NFA to change states "for free."

Let's modify our first example to include epsilon transitions:

   ┌─────┐    1     ┌─────┐    0,1   ┌─────┐    0,1   ┌─────┐
-->│ q0  │───────-->│ q1  │───────-->│ q2  │───────-->│ q3  │
   └─────┘    ↺     └─────┘          └─────┘          └─────┘
     │ 0,1      ε                                      (accept)
     │        ┌─────┐     1    ┌─────┐
     └───────>│ q4  │────────>│ q5  │
              └─────┘         └─────┘
                               (accept)

With these epsilon transitions:

• The NFA can now also accept the string "1" by moving from q0 to q4 (via ε-transition) and then to q5 on reading '1'.
• This modification expands the language recognized by the NFA without significantly complicating the state diagram.

NFA vs. DFA: Comparing Capabilities

Despite their apparent differences, NFAs and DFAs are equivalent in terms of the languages they can recognize. This equivalence leads to several important observations:

1. Regular Languages: Both NFAs and DFAs recognize regular languages.
2. Convertibility: Any NFA can be converted to an equivalent DFA, and vice versa.
3. Simplicity vs. Determinism: NFAs often allow for simpler and more intuitive designs, while DFAs provide deterministic behavior.
4. State Explosion: Converting an NFA to a DFA can potentially lead to an exponential increase in the number of states.

The Power of Nondeterminism

While NFAs don't extend the set of recognizable languages beyond what DFAs can handle, they offer several advantages:

1. Compact Representation: NFAs can often represent certain languages with fewer states than equivalent DFAs.
2. Intuitive Design: The nondeterministic nature of NFAs can make it easier to design automata for complex patterns.
3. Flexibility: Epsilon transitions and multiple possible paths provide more flexibility in automaton design.

Formal Properties of NFAs

Let's delve deeper into the formal aspects of NFAs to better understand their behavior and capabilities.

Transition Function

The transition function δ in an NFA is defined as:

δ: Q × (Σ ∪ {ε}) → P(Q)

Where:

• Q is the set of states
• Σ is the input alphabet
• ε represents the empty string
• P(Q) is the power set of Q (set of all subsets of Q)

This definition allows for:

1. Multiple next states for a given input and current state
2. Transitions on the empty string (ε-transitions)
3. The possibility of no next state (represented by an empty set)

Extended Transition Function

To handle strings of input symbols, we define an extended transition function δ* as follows:

δ*(q, w) = { p | there exists a path from q to p labeled w }

Where:

• q is the starting state
• w is the input string
• p is any state reachable from q by following transitions labeled with symbols from w (including ε-transitions)

Language Recognition

An NFA N = (Q, Σ, δ, q0, F) recognizes a language L(N) defined as:

L(N) = { w ∈ Σ* | δ*(q0, w) ∩ F ≠ ∅ }

In other words, a string w is accepted by the NFA if there exists at least one path from the start state q0 to any accept state in F, consuming all symbols of w.

Algorithms and Techniques for NFAs

Working with NFAs involves several important algorithms and techniques:

1. NFA Simulation

Simulating an NFA on an input string involves tracking all possible current states at each step. This can be done using a set of active states:

1. Initialize the set of active states with the start state and all states reachable via ε-transitions.
2. For each input symbol: a. Compute the set of next states for all active states. b. Add all states reachable via ε-transitions from the computed next states.
3. Accept if the final set of active states contains an accept state.

2. NFA to DFA Conversion (Subset Construction)

Converting an NFA to an equivalent DFA involves the subset construction algorithm:

1. Start with the ε-closure of the NFA's start state as the DFA's start state.
2. For each DFA state (representing a set of NFA states) and each input symbol: a. Compute the set of NFA states reachable from the current set. b. Take the ε-closure of this set to form a new DFA state.
3. Mark a DFA state as accepting if it contains any accepting NFA state.

3. Regular Expression to NFA Conversion (Thompson's Construction)

Thompson's construction algorithm converts a regular expression to an equivalent NFA:

1. For each symbol and operator in the regular expression, construct a small NFA.
2. Combine these NFAs using ε-transitions according to the structure of the regular expression.

Applications of NFAs

NFAs find applications in various areas of computer science and software engineering:

1. Pattern Matching: NFAs are used in implementing regular expression engines, crucial for text processing and search operations.

2. Lexical Analysis: Compiler front-ends use NFAs to recognize tokens in the source code.

3. Protocol Specification: Communication protocols can be modeled and verified using NFAs.

4. Natural Language Processing: Certain aspects of language models and parsers utilize NFA concepts.

5. DNA Sequence Analysis: Bioinformatics applications use NFA-like structures for pattern matching in genetic sequences.

Limitations and Extensions

While NFAs are powerful tools, they have limitations:

1. Non-determinism Overhead: Simulating an NFA can be less efficient than running an equivalent DFA.

2. Limited Expressiveness: Like DFAs, NFAs can only recognize regular languages, not context-free or more complex languages.

To address these limitations, various extensions have been proposed:

1. Pushdown Automata (PDA): Extend NFAs with a stack, allowing recognition of context-free languages.

2. Probabilistic Automata: Incorporate probabilities into transitions, useful for modeling uncertain systems.

3. Quantum Finite Automata: Leverage quantum superposition to explore multiple computation paths simultaneously.

Conclusion

Nondeterministic Finite Automata represent a fascinating and powerful concept in the theory of computation. While they don't extend the class of recognizable languages beyond regular languages, they offer a more flexible and often more intuitive approach to designing automata for various problems.

Key takeaways include:

1. NFAs allow multiple possible next states and ε-transitions, unlike DFAs.
2. The languages recognized by NFAs are exactly the regular languages.
3. Any NFA can be converted to an equivalent DFA, and vice versa.
4. NFAs often provide more compact and intuitive representations of certain languages.
5. The study of NFAs leads to important algorithms in automata theory and practical applications in areas like pattern matching and compiler design.

As we continue to explore more advanced concepts in theoretical computer science, the understanding of NFAs serves as a crucial foundation. Whether you're designing a regex engine, analyzing protocols, or delving deeper into computational theory, the principles of NFAs will undoubtedly prove valuable in your journey through the fascinating world of computer science.

Article created from: https://www.youtube.com/watch?v=W8Uu0inPmU8&list=PLhqug0UEsC-IDomfNsn8e3neoy34o8oye&index=4