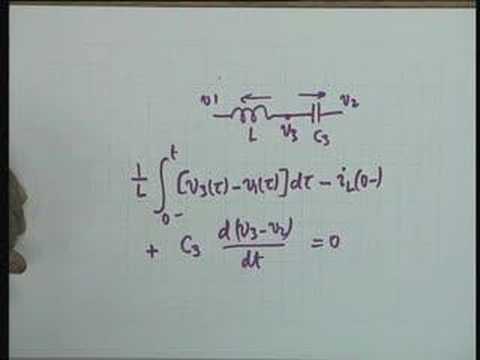
Create articles from any YouTube video or use our API to get YouTube transcriptions
Start for freeIntroduction to Network Equations
In circuit analysis, there are two primary methods for writing network equations:
- Mesh analysis
- Node analysis
Both methods allow us to solve for unknown currents and voltages in a circuit. The choice between mesh and node analysis often depends on which method requires fewer equations for a given circuit.
Mesh Analysis
Mesh analysis involves identifying closed paths in a circuit called meshes and writing equations based on Kirchhoff's Voltage Law (KVL) for each mesh.
Key Points:
- A mesh is the smallest closed path that does not contain any other closed path within it
- All meshes are loops, but not all loops are meshes
- The number of independent mesh equations required is: B - N + 1 Where B = number of branches, N = number of nodes
- Each circuit element must be included in at least one mesh equation
Example of Mesh Analysis
Let's consider a circuit with two meshes:
+ L C1 R1
e(t) --- ))) ---||--- /\/\/\ ---+
- |
C2 |
---||--- |
L2 |
))) |
|
R2
/\/\/\
|
---
GND
For this circuit, we would write two mesh equations:
-
For mesh 1 (i1): e(t)u(t) = L(di1/dt) + (1/C1)∫i1dt + R1(i1-i2) + (1/C2)∫(i1-i2)dt
-
For mesh 2 (i2): 0 = L2(di2/dt) + R2i2 + (1/C2)∫(i2-i1)dt + R1(i2-i1)
Node Analysis
Node analysis involves writing equations based on Kirchhoff's Current Law (KCL) for each node in the circuit, except for the reference node (usually ground).
Key Points:
- The number of independent node equations required is: N - 1 Where N = number of nodes
- Node voltages are measured with respect to a reference node
Example of Node Analysis
Consider a circuit with three nodes:
i(t)u(t)
|
R0
|
+---+---+
| |
C0 R1
| |
| L1
| |
+---+---+
|
C1
|
R2
|
GND
For this circuit, we would write three node equations:
-
For node 1 (V1): i(t)u(t) = V1/R0 + C0(dV1/dt) + (V1-V2)/R1 + (1/L)∫(V1-V3)dt
-
For node 2 (V2): 0 = (V2-V1)/R1 + C1(dV2/dt) + V2/R2
-
For node 3 (V3): 0 = (1/L)∫(V3-V1)dt + C1(d(V3-V2)/dt)
Initial Conditions
When solving differential equations derived from circuit analysis, we need to consider initial conditions. These are typically evaluated at t = 0+, just after a switch is closed or a source is applied.
Methods for Finding Initial Conditions:
- Physical considerations
- From the differential equations themselves
Example: RC Circuit
For a simple RC circuit with a voltage source V switched on at t=0:
+ R
V --- /\/\/\ ---+
- |
C
|
---
GND
- i(0+) = V/R (capacitor acts as a short circuit initially)
- di/dt(0+) = -V/(R^2C) (found by differentiating the circuit equation)
Steady-State Solutions
The steady-state solution is the long-term behavior of the circuit as t approaches infinity. For DC sources, this often involves treating inductors as short circuits and capacitors as open circuits.
Sinusoidal Steady-State
For sinusoidal sources, we can use phasor analysis to find the steady-state solution without solving differential equations.
Example: Current source parallel with RC
i0sin(ω0t)u(t)
|
+---+---+
| |
R C
| |
+---+---+
|
GND
The voltage across the parallel RC combination can be found using phasor analysis:
V(t) = (i0 / √(G^2 + (ω0C)^2)) * sin(ω0t - tan^(-1)(ω0C/G))
Where G = 1/R
Conclusion
Understanding how to write and solve network equations using mesh and node analysis is crucial for circuit analysis. By considering initial conditions and steady-state solutions, engineers can fully describe the behavior of a circuit over time. For sinusoidal sources, phasor analysis provides a powerful tool for finding steady-state solutions without solving complex differential equations.
Article created from: https://youtu.be/gk7HNFBXi_c?si=ONobVY576AjK6lyP


