Mastering Matrices in Mathematics

Understanding the Basics of Matrices

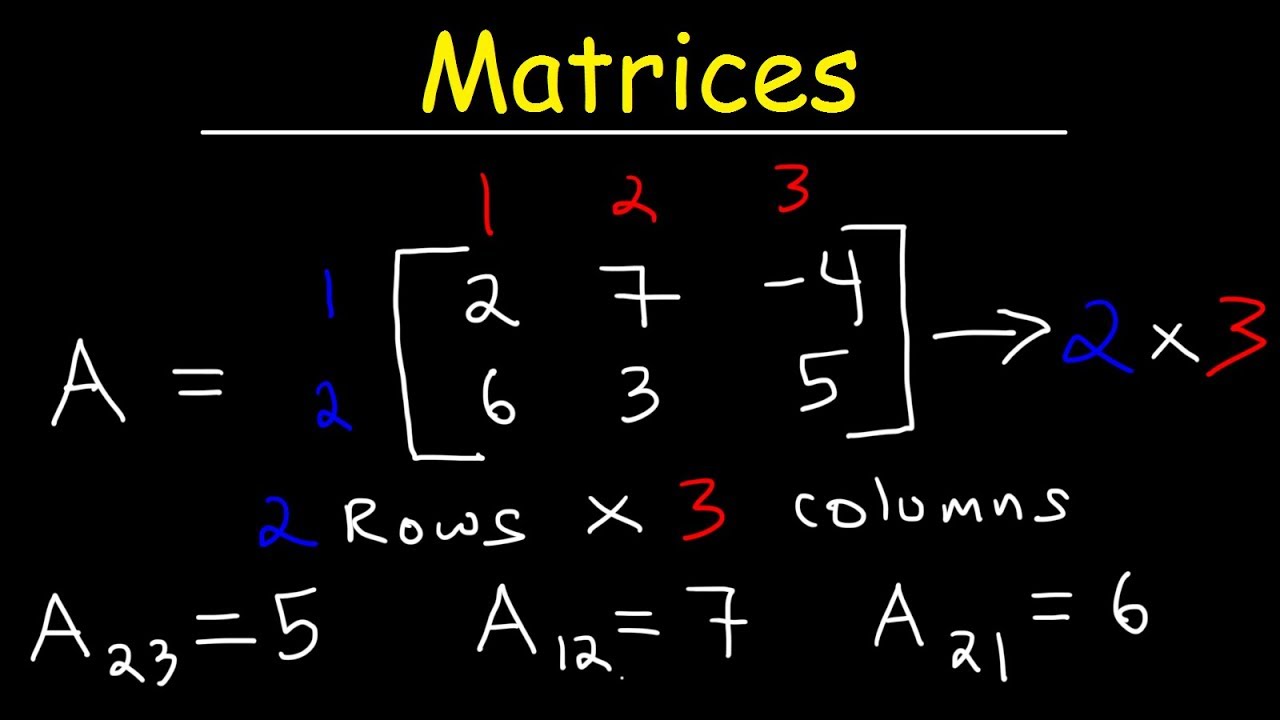
A matrix is an organized array of numbers arranged in rows and columns. It's a fundamental concept in mathematics and various applications like computer science, physics, and engineering. The arrangement of a matrix is defined by its order, which specifies the number of rows followed by the number of columns.

Identifying Matrix Order

For instance, consider a matrix labeled as Matrix A with elements 2, 7, -4 in the first row and 6, 3, 5 in the second row. This matrix has two rows and three columns, making it a 2x3 matrix. The order is crucial as it helps in defining the size and capabilities of a matrix.

Locating Specific Elements

Each element in a matrix can be identified using its position. For example, element A23 refers to the element located at the second row and third column of Matrix A. In this case, it's the number 5. Similarly, element A12 is found at first row second column with a value of 7.

Operations on Matrices

Adding Matrices

To add two matrices like Matrix A (2x3) with elements [2, 3, 5; -4] and Matrix B (also a 2x3) with elements [7, 4; -3], you simply add corresponding elements together. The result for our example would be:

• First element (first row first column): 2 + 7 = 9
• Second element (first row second column): 3 + 4 = 7
• And so forth. This operation requires that both matrices have the same order.

Multiplying Elements by a Scalar

Multiplying each element by a scalar involves taking every individual number in the matrix and multiplying it by that scalar. For instance, multiplying every element of Matrix A by four results in new values:

• First element becomes 4 * 2 = 8
• Second element becomes 4 * 3 = 12
• And so on for each element within the matrix.

Subtracting Matrices

Subtraction follows a similar pattern to addition but involves taking the difference between corresponding elements from two matrices. Using our previous example matrices:

• First result (first row first column): 2 - 7 = -5 The subtraction shows how matrices can also represent transformations or changes between different states or configurations.

Practical Exercises with Various Matrices

The video also introduces other matrices labeled C through H with varying orders:

• Matrix C: A square matrix due to its equal number of rows and columns (2x2).
• Matrix D: Not square since it has three rows but only two columns (3x2). The concept of square matrices is important because they often have special properties in mathematical applications such as determinant calculation or eigenvalue problems. The tutorial encourages viewers to practice identifying orders themselves which reinforces learning through active participation. The video concludes with links for further learning resources available online which viewers can access to deepen their understanding or clarify any doubts regarding pre-calculus topics including more complex operations involving matrices.

Article created from: https://youtu.be/yRwQ7A6jVLk?si=ODbGQlarbYDFPXRs